研究組織・メンバー

A03:カオス的な自己組織化臨界としての位相連鎖の数理機構

研究代表者
末谷大道・大分大学理工学部・教授
WEBhttp://www.nature.oita-u.ac.jp/suetani.html

紹介文本文

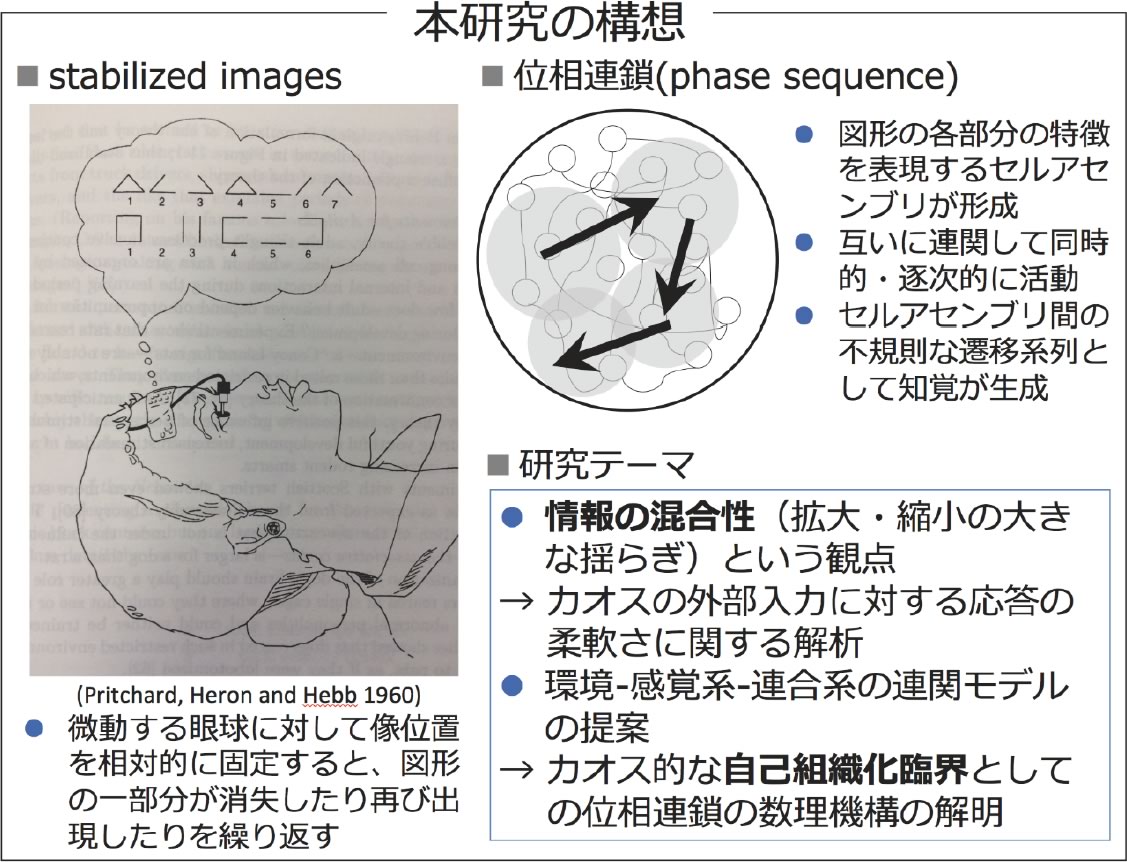
Hebbは、自発性脳活動が知覚の汎化・記憶の安定性・注意の変わりやすさなどの機能にどのように関わるのか、という問いを通じて、ヘッブ学習・セルアセンブリなどの巨視的な心理現象と微視的な神経生理機構を結びつける重要な諸仮説を呈示した。特に、白内障などの理由による先天的な盲患者が開眼手術を受けた後の視覚学習に関する多数の症例報告を通じて、知覚を局所的な特徴を表現するセルアセンブリ同士が連関しそれらの間を不規則に遷移し続ける現象として捉え、これを位相連鎖（phase sequence）と呼んだ。そして、この位相連鎖は知覚に留まらず、異なる概念間を飛躍して繋ぐことの出来る高度な思考能力の源になっていると考えた。近年の研究では、例えば、Kenetらは麻酔下ネコの視覚系において無刺激下での自発性活動が方位選択コラムに類似し、長時間スケールで異なるコラム間を遷移することを発見した。また、理論面においては、津田らが海馬の数理モデルを構築し、CA3で生成するカオス的遍歴現象がCA1 における縮小ダイナミクスを駆動することによってカントール集合上にエピソード記憶が形成されることを示すなど、Hebbのシナリオを示唆する報告がなされるようになってきた。
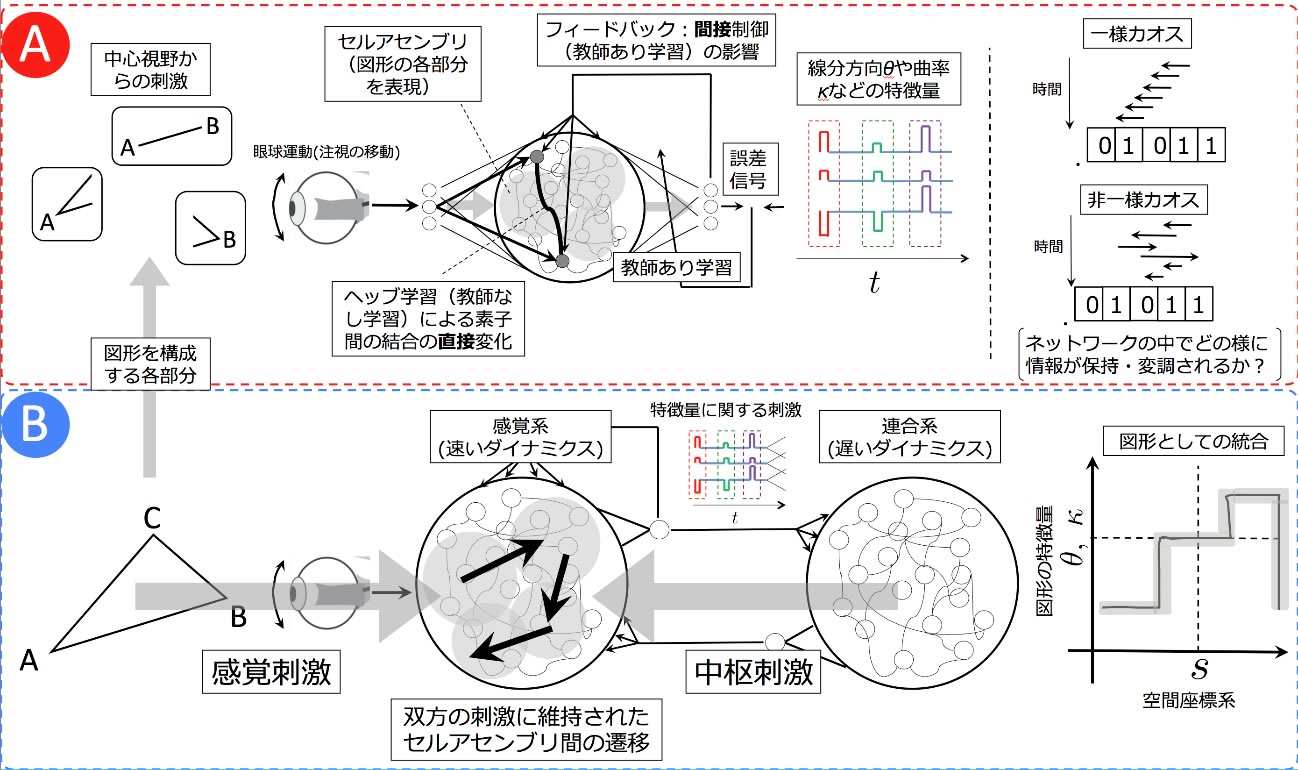
このような背景の下、本研究では、位相連鎖の形成に関する数理的な仕組みについて非線形動力学の立場から明らかにする。まず、外部から時系列入力を受ける際に神経回路網内に伝播する情報の流れと混合性について、ダイナミクスをビット空間に展開したときの相互情報量や転送エントロピーによって解析し、外部入力に対してカオスが持つ応答の柔軟性を捉える新たな方法を提案する。次に、外部入力を受ける二つの再帰型神経回路網が結合した系として環境（刺激の発生源）・感覚系（「速い」ダイナミクス）・連合系（「遅い」ダイナミクス）の連関をモデル化し、位相連鎖の発生を自己組織化臨界現象として理解する。

文献

1. H. Suetani. (2017)
Assimilating nonlinear dynamics with FORCE-learning : A perspective from chaotic synchronization.
in Proceedings of International Symposium on Nonlinear Theory and Its Applica- tions. (NOLTA): pp268-270.
H. Suetani. (2015)
Weak Sensitivity to Initial Conditions for Generating Temporal Patterns in Recurrent Neural Networks: A Reservoir Computing Approach.
Interdisciplinary Symposium on Complex Systems. 14: pp. 47–55, Springer International Publishing.
U. Parlitz, H. Suetani, S. Luther. (2013)
Identification of Equivalent Dynamics using Ordinal Pattern Distributions.
The European Physical Journal Special Topics. 222: 553-568.  
H. Suetani, K. Soejima, R. Matsuoka, U. Parlitz, H. Hata. (2012)
Manifold Learning Approach for Chaos in the Dripping Faucet.
Physical Review. E 86: 036209 [8 pages].